1999 - 2017 : saros 145
Une histoire de Saros
L'histoire se répète, c'est bien connu.
L'éclipse totale du 21/08/2017 appartient au Saros 145, tout comme l'était l'éclipse du 11 août 1999 qui était visible en France, et en Europe plus généralement.
Allez-vous transformer l'essai de l'éclipse '99 ?
Allez-vous prendre votre revanche sur '99 ?
Allez-vous perdre encore sur la '99 devant l'éternel ?
These are the questions...
Allez-vous prendre votre revanche sur '99 ?
Allez-vous perdre encore sur la '99 devant l'éternel ?
These are the questions...
Connaissez-vous le Saros ?
La treizième éclipse totale du XXIe siècle (dix auparavant plus deux hybrides) a déjà eu lieu, et elle se reproduira encore et encore…
En effet, toutes les éclipses sont soumises à un cycle implacable de 18 années 11 jours et 8 heures environ que l'on nomme Saros.
Deux éclipses séparées par une période équivalente au Saros sont tout à fait similaires géométriquement : Terre et Lune sont à la même distance et leurs positions relatives au Soleil sont identiques.
Cela ne signifie pas pour autant qu’une éclipse soit visible au même endroit du globe tous les Saros. En raison des 8 heures contenues dans ce cycle (un tiers d’une journée), l’éclipse se décale sur le globe d’un tiers (120°) : la même configuration a lieu par contre tous les 3 saros (soit tous les 54 ans et 34 jours si vous savez compter) aux mêmes longitudes, mais pas aux mêmes latitudes. C'est compliqué à expliquer simplement…
Deux éclipses séparées par une période équivalente au Saros sont tout à fait similaires géométriquement : Terre et Lune sont à la même distance et leurs positions relatives au Soleil sont identiques.
Cela ne signifie pas pour autant qu’une éclipse soit visible au même endroit du globe tous les Saros. En raison des 8 heures contenues dans ce cycle (un tiers d’une journée), l’éclipse se décale sur le globe d’un tiers (120°) : la même configuration a lieu par contre tous les 3 saros (soit tous les 54 ans et 34 jours si vous savez compter) aux mêmes longitudes, mais pas aux mêmes latitudes. C'est compliqué à expliquer simplement…
Ce n’est pas nouveau ! Les Chinois ont découvert au XXIIè siècle avant notre ère un tel cycle de 19 ans ce qui est tout à fait épatant.
Plus récemment, le grec Méton en 432 av J.-C. a trouvé pour le cycle la valeur de 6940 jours au lieu de 6585,32 jours précisément.
Plus récemment, le grec Méton en 432 av J.-C. a trouvé pour le cycle la valeur de 6940 jours au lieu de 6585,32 jours précisément.
Ce cycle métonique (de Méton) permettait de prédire les éclipses mais seulement approximativement et sur une durée assez courte.
Quant au Saros, il est réglé comme une horloge atomique, la précision d'une montre suisse…
Ce cycle résulte de l’harmonisation de trois cycles lunaires…
Ce cycle résulte de l’harmonisation de trois cycles lunaires…
- Cycle du Mois synodique * :
29.53059 jours = 29j 12h 44m
- Cycle du Mois draconitique (de nœud à nœud) ** :
27.21222 jours = 27j 05h 06m
- Cycle du Mois anomalistique (de périgée à périgée) *** :
27.55455 jours = 27j 13h 19m
29.53059 jours = 29j 12h 44m
- Cycle du Mois draconitique (de nœud à nœud) ** :
27.21222 jours = 27j 05h 06m
- Cycle du Mois anomalistique (de périgée à périgée) *** :
27.55455 jours = 27j 13h 19m
=> Un Saros est égal à 223 mois synodiques, 242 mois draconitiques et 239 mois anomalistiques.
* C’est le temps séparant deux nouvelles Lunes
** C’est le temps entre deux passages de la Lune au même nœud de son orbite ; les nœuds sont les points où l'orbite lunaire coupent le plan de l'orbite de la Terre
*** C’est le temps séparant deux passages successifs de la Lune au périgée. La distance entre la Terre et la Lune varie entre 356375 km (périgée) et 406720 km (apogée).
** C’est le temps entre deux passages de la Lune au même nœud de son orbite ; les nœuds sont les points où l'orbite lunaire coupent le plan de l'orbite de la Terre
*** C’est le temps séparant deux passages successifs de la Lune au périgée. La distance entre la Terre et la Lune varie entre 356375 km (périgée) et 406720 km (apogée).
A quoi sert le saros ?
Le saros permet ainsi de prédire les éclipses futures, mais aussi les éclipses passées pour les historiens !
Mais alors… d’où vient le nom Saros ?
Origine un peu maladroite et obscure… mais en parlant d’éclipses ça tombe plutôt bien !
Cela proviendrait d’une erreur d’Edmund Halley, découvreur de la comète éponyme qui lut une définition du terme saros dans une encyclopédie byzantine du Xe siècle qui n’avait alors rien à voir avec les éclipses.
En outre, le terme « sar » a la signification d’ «univers » chez les sumériens.
Origine un peu maladroite et obscure… mais en parlant d’éclipses ça tombe plutôt bien !
Cela proviendrait d’une erreur d’Edmund Halley, découvreur de la comète éponyme qui lut une définition du terme saros dans une encyclopédie byzantine du Xe siècle qui n’avait alors rien à voir avec les éclipses.
En outre, le terme « sar » a la signification d’ «univers » chez les sumériens.
Le saros 145 ?
L’éclipse du 21 août 2017 appartient au Saros n° 145, et voici ses particularités :
Toutes les précisions sont disponibles ici :
http://eclipse.gsfc.nasa.gov/SEsaros/SEsaros145.html
http://eclipse.gsfc.nasa.gov/SEsaros/SEsaros145.html
Ce Saros dure 1370,29 années et comporte 77 éclipses de Soleil dont 41 sont totales.
La première éclipse du Soleil de ce cycle a eu lieu le 4 janvier 1639 après J.-C. et la dernière aura lieu le 17 avril 3009 après J.-C.
La précédente éclipse du saros 145 a eu lieu le 11 août 1999 notamment en France et la prochaine aura lieu le 2 septembre 2035 visible au Japon, en Corée et en Chine.
Afin de mieux se représenter ce qu’est un saros… voici l'animation du saros 145 en gif animé.
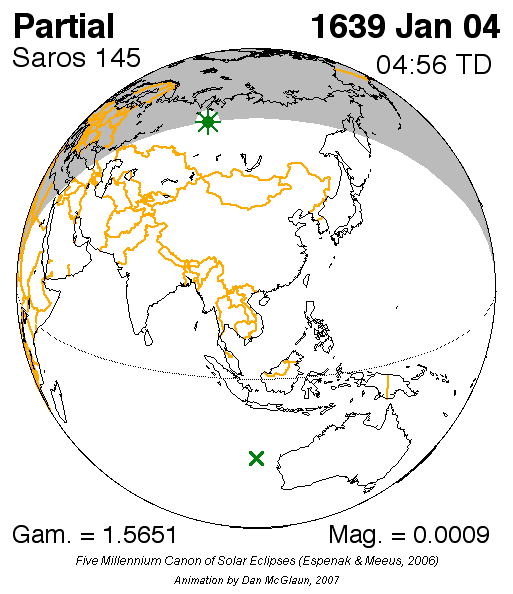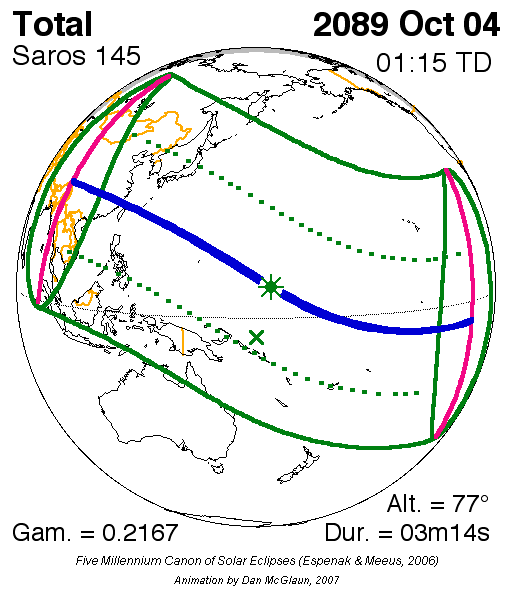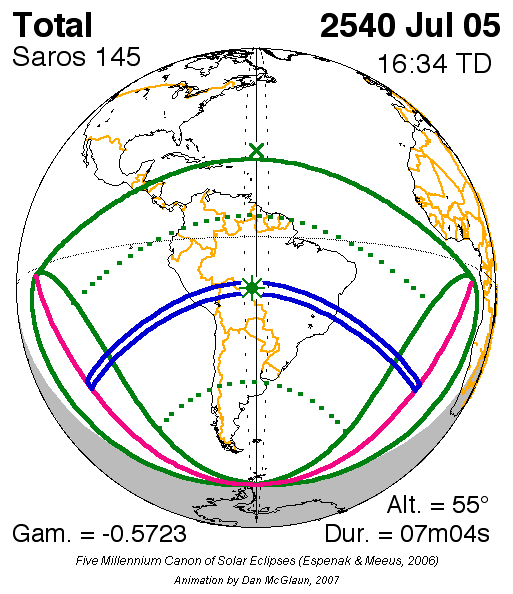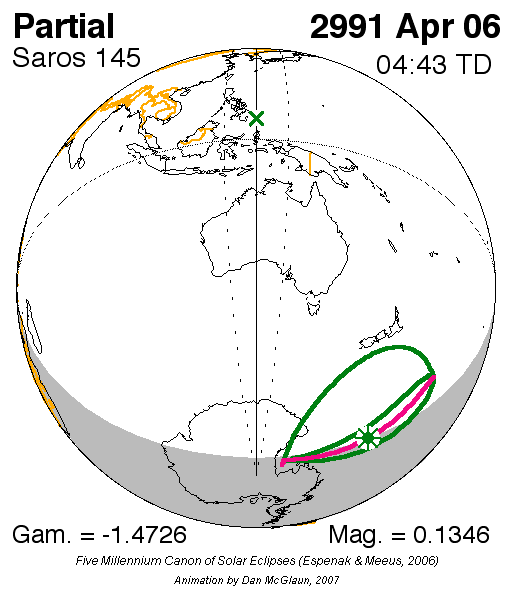
Pour aller plus loin...
Rappelez-vous, une éclipse de Soleil correspond à une position géométrique très particulière et se répète ainsi dans la même configuration tous les 18 ans 11 jours 8 heures environ.
Et lorsque deux éclipses de Soleil sont espacées d'une période d'un saros, elles sont géométriquement similaires.
Ces deux éclipses se déroulent alors quasiment à la même époque de l'année, la Lune est quasiment à la même distance de la Terre, et la Lune est au même noeud* sur son orbite autour de la Terre.
* Il existe deux noeuds (ascendant et descendant), cela correspond à l'intersection du plan orbital lunaire autour de la Terre et du plan terrestre (plan de l'écliptique autrement dit).
Et lorsque deux éclipses de Soleil sont espacées d'une période d'un saros, elles sont géométriquement similaires.
Ces deux éclipses se déroulent alors quasiment à la même époque de l'année, la Lune est quasiment à la même distance de la Terre, et la Lune est au même noeud* sur son orbite autour de la Terre.
* Il existe deux noeuds (ascendant et descendant), cela correspond à l'intersection du plan orbital lunaire autour de la Terre et du plan terrestre (plan de l'écliptique autrement dit).
Les 8 heures dans la durée du Saros ont leur importance car 8h = 1/3 de 24h (1/3 de journée).
C'est ce qui explique qu'à chaque nouveau Saros, l'éclipse se déplace d'1/3 en longitude vers l'ouest sur le globe terrestre comme vous pouvez le voir sur la carte ci-après.
Au bout de 3 saros, on pourrait donc s'attendre à voir exactement le même tracé d'éclipse, mais ce n'est pas tout à fait le cas.
C'est ce qui explique qu'à chaque nouveau Saros, l'éclipse se déplace d'1/3 en longitude vers l'ouest sur le globe terrestre comme vous pouvez le voir sur la carte ci-après.
Au bout de 3 saros, on pourrait donc s'attendre à voir exactement le même tracé d'éclipse, mais ce n'est pas tout à fait le cas.
Cette carte ci-après comprend 6 tracés d'éclipses du saros 145 (réalisés à partir du site de Xavier Jubier).
- L'éclipse totale de Soleil du 20 juillet 1963 qui était visible au Japon, Alaska, Canada, Etats-Unis ;
- L'éclipse totale de Soleil du 31 juillet 1981 qui était visible au Kazakhstan et Russie ;
- L'éclipse totale de Soleil du 11 août 1999 qui était visible en Europe, dont la France, au Moyen-Orient et en Inde ;
- L'éclipse totale de Soleil du 21 août 2017 qui sera visible aux USA exclusivement ;
- L'éclipse totale de Soleil du 2 septembre 2035 qui sera visible en Chine, en Corée et au Japon ;
- L'éclipse totale de Soleil du 12 septembre 2053 qui sera visible en Espagne, au Maghreb, et au proche-Orient.
- L'éclipse totale de Soleil du 20 juillet 1963 qui était visible au Japon, Alaska, Canada, Etats-Unis ;
- L'éclipse totale de Soleil du 31 juillet 1981 qui était visible au Kazakhstan et Russie ;
- L'éclipse totale de Soleil du 11 août 1999 qui était visible en Europe, dont la France, au Moyen-Orient et en Inde ;
- L'éclipse totale de Soleil du 21 août 2017 qui sera visible aux USA exclusivement ;
- L'éclipse totale de Soleil du 2 septembre 2035 qui sera visible en Chine, en Corée et au Japon ;
- L'éclipse totale de Soleil du 12 septembre 2053 qui sera visible en Espagne, au Maghreb, et au proche-Orient.
Cliquez sur la map pour l'agrandir (réalisée avec le site de Xavier Jubier).
Saros 145
Les éclipses de 1963 et 2017 sont à peu près équivalentes en longitude.
Les éclipses de 1981 et 2035 sont à peu près équivalentes en longitude.
Les éclipses de 1999 et 2053 sont à peu près équivalentes en longitude.
Les éclipses de 1981 et 2035 sont à peu près équivalentes en longitude.
Les éclipses de 1999 et 2053 sont à peu près équivalentes en longitude.
D'où vient cet à peu près en longitude ?
Le tiers de journée évoqué plus haut n'est pas vraiment 1/3 mais approximativement (,32117 et non pas 0,33333...).
Le tiers de journée évoqué plus haut n'est pas vraiment 1/3 mais approximativement (,32117 et non pas 0,33333...).
Et pourquoi les latitudes diffèrent aussi ?
C'est lié aux anomalies orbitales de la Lune sur sa ligne des noeuds qui n'est pas fixe et dont la période est égale à 18,6 années environ.
C'est plutôt compliqué, mais si vous souhaitez en savoir plus sur la précession de la ligne des noeuds, je vous invite à lire l'excellent article rédigé par un professionnel de l'IMCCE (Patrick Rocher de l'Institut de Mécanique Céleste et de Calcul des Ephémérides) pour le grand public à cette adresse :
http://www.imcce.fr/fr/grandpublic/systeme/promenade/pages3/386.html.
Au passage, vous réviserez un peu vos connaissances sur les éclipses en général...
C'est lié aux anomalies orbitales de la Lune sur sa ligne des noeuds qui n'est pas fixe et dont la période est égale à 18,6 années environ.
C'est plutôt compliqué, mais si vous souhaitez en savoir plus sur la précession de la ligne des noeuds, je vous invite à lire l'excellent article rédigé par un professionnel de l'IMCCE (Patrick Rocher de l'Institut de Mécanique Céleste et de Calcul des Ephémérides) pour le grand public à cette adresse :
http://www.imcce.fr/fr/grandpublic/systeme/promenade/pages3/386.html.
Au passage, vous réviserez un peu vos connaissances sur les éclipses en général...
Du fait de ce décalage en latitude, les séries d'éclipses et leurs Saros ont un début et une fin.
Si vous venez de lire, bravo pour votre ténacité et merci de laisser un commentaire pour me le faire savoir
Si vous venez de lire, bravo pour votre ténacité et merci de laisser un commentaire pour me le faire savoir
Pour conclure…
L’homme peut profiter de ce spectacle céleste pendant quelques siècles et millénaires mais pas plus car la Lune s’éloignant de la Terre d’un demi centimètre tous les ans, elle apparaîtra trop lointaine pour provoquer des éclipses totales de Soleil, mais nous le savons… le temps nous est compté.
Ajouter un commentaire
Date de dernière mise à jour : 29/12/2016



